2.7 Frekvenčné charakteristiky

Ak budeme budiť sústavu signálom x1(t)=sin ωt a meniť ω, dostaneme pre rôzne hodnoty ω rôzne amplitúdy a fázy frekvenčného prenosu. Ak vynesieme závislosť amplitúdy a fázy vektora prenosu od ω, dostaneme frekvenčnú charakteristiku (AFCH, FFCH).

1.) Frekvenčná charakteristika v komplexnej rovine

Do komplexnej roviny kreslíme vektory prenosu člena pre ωε<0;¥). Dĺžka vektora určuje absolútnu hodnotu prenosu (amplitúdu) |G(jω)|. Uhol medzi vektorom a kladnou časťou reálnej osi je fáza prenosu (φ), čiže fázový posun medzi vstupným a výstupným signálom člena pri danej ω. Kreslíme len vrcholy vektorov a ich spojením dostaneme frekvenčnú charakteristiku (ociachovanú cez ω). Frekvenčná charakteristika člena je v komplexnej rovine čiara spájajúca konce vektorov prislúchajúcich frekvenciám ω<0;¥).

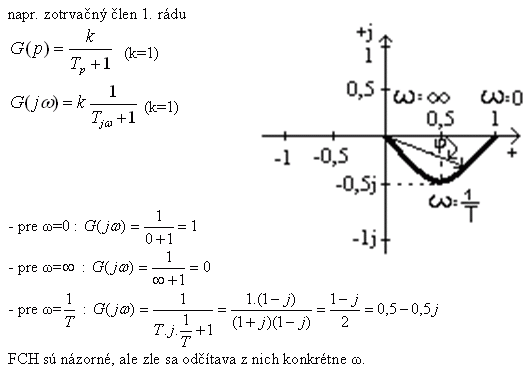
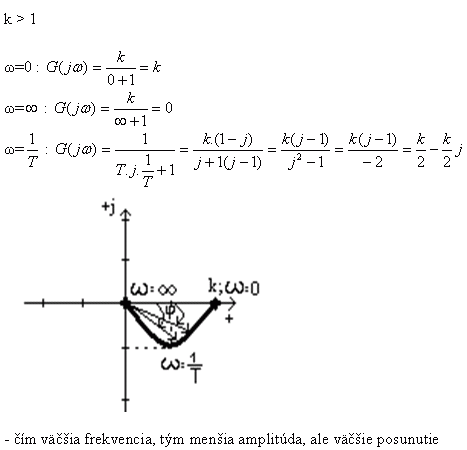
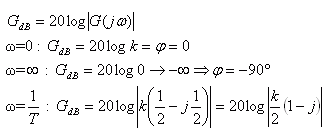
Logaritmické frekvenčné charakteristiky sú výhodnejšie ako frekvenčné charakteristiky v komplexnej rovine pre ľahšie a jasnejšie čítanie ω. Priebeh amplitúdovej frekvenčnej charakteristiky aproximujeme (nahrádzame) lomenou čiarou. Uhlové frekvencie lomu sú určené prevrátenou hodnotou časovej konštanty T. Pri frekvencii lomu je rozdiel medzi skutočnou a aproximovanou charakteristikou 3dB.

Platí: - ak je AFCH rovnobežná s osou ω → φ= 0º

- ak AFCH klesá o 20dB/dek → φ= -90º

- ak AFCH klesá o 40dB/dek → φ= -180º

- ak AFCH stúpa o 20dB/dek → φ= +90º

- ak AFCH stúpa o 30dB/dek → φ= +180º

To umožňuje nakresliť FFCH rovno zo známej AFCH (lebo FFCH sa zle meria a AFCH sa dá ľahko merať).

Ďalšou výhodou týchto charakteristík je, že pri sériovo zapojených členoch je AFCH s FFCH grafickým súčtom jednotlivých charakteristík.