Na počiatku vývoja inteligentných systémov stálo mnoho vedcov z rôznych oblastí vedy. Za zmienku stoja tri mená:
1.) J. Lukasewicz (a jeho tým), ktorý dal základy viachodnotovej logike ,
2.) L. Zadeh, ktorý položil základy tzv. fuzzy-množinám ,
3.) Ymakawa, ktorý vyrobil prvé VLSI fuzzy-obvody, čím umožnil realizáciu teoretických prác.
Bežná regulačná technika dokáže reagovať na vopred popísané stavy (popísané napr. diferenciálnymi rovnicami) vopred známymi spôsobmi. Avšak fuzzy regulátory, kvalitatívne regulátory, neurónové siete, expertné systémy reálneho času vo funkcii regulátorov, nepotrebujú model systému vo forme diferenciálnych rovníc a nemusia sa opierať o algoritmický postup. Môžu využívať rôzne heuristiky (praxou overené a zaznamenané postupy), osobné skúsenosti, verbálne vzdielané skúsenosti často vo veľmi vágnej a niekedy konfliktnej forme (niektoré výroky si môžu aj odporovať). Mnohé z týchto ,,inteligentných” regulátorov používajú, namiesto modelu vo forme diferenciálnych rovníc, pravidlo AK, POTOM.
Ak podrobíme rozboru činnosť človeka riadiaceho nejaký systém, je možné v jeho činnosti rozlíšiť niekoľko úrovní. Na najnižšej úrovni používa operátor naučených dynamických stereotypov. Príkladom môže byť pilot lietadla alebo vodič automobilu. U skúsených pilotov a vodičov prebieha za normálnej situácie riadenie celkom reflexívne, mimo priestoru vôle a intenzívneho sústredenia. Riadenie tu prebieha v reálnom čase, s pomerne veľkou presnosťou a človek pracuje a človek pracuje ako regulátor v slučke spätnej väzby.
Nasledujúca vyššia úroveň je riadenie založené na pravidlách, ktoré umožňujú výber naučených stereotypov. Vodič naučený na prevoz vpravo musí pri jazde v Anglicku uvažovať nad svojimi reakciami a nemôže jednať automaticky, ako bol zvyknutý. Rovnako aj pilot napr. v turbulencii musí prejsť na stereotypy riadenia. Podobne je tomu aj pri zhoršenej viditeľnosti atď. Na tejto úrovni však stále existujú súbory pravidiel, ktoré umožňujú nájsť riešenie takmer ľubovoľnej dopravnej situácie. (Na tejto úrovni vlastne pomocou pravidiel vyberáme a spúšťame príslušné stereotypy. Riadime sa pravidlami AK... POTOM – AK prídeš na križovatku a chceš odbočiť vpravo, POTOM musíš skončiť na ľavej strane bočnej ulice.
Treťou úrovňou je riadenie na základe hlbších znalostí a súvislostí, ktoré vyžaduje plánovanie činnosti, rozhodovanie, myšlienkové experimenty apod., kde sme postavený do situácie, pre ktorej riešenie nemáme vopred známe pravidlá. Na tejto úrovni existuje spravidla niekoľko možných variant riešenia (niekedy dokonca rovnocenných) a máme s pravidla málo informácií pre racionálne rozhodnutie. Na tejto úrovni je rozhodovanie či plánovanie založené na veľmi nepresných údajoch.
Intuitívne je zrejmé, že čím vyššia úroveň riadenia, tým vyššia inteligencia, ale tým menšia presnosť alebo väčšia neurčitosť (obvykle aj vyššia zodpovednosť, pretože tomu môžu zodpovedať aj závažnejšie následky).
Pokiaľ budeme hovoriť o inteligentných regulátoroch, budeme mať na mysli tie, ktoré pracujú na druhej alebo tretej úrovni. Takisto však môže fuzzy alebo iný typ inteligentného regulátora nahradiť trojpolohový regulátor alebo PID-regulátor. Výsledok však spravidla nebude lepší. Na druhej strane, ak budeme pracovať v zle alebo príliš determinovaných systémoch, obrátené dosadenie je nemysliteľné.
Tie najdôležitejšie prípady, kedy je užitočné použiť niektorý z prístupov, ktoré spojujeme s inteligentnými regulátormi, sú:
1.) Pokiaľ pracujeme s nesymetrickými a fuzzy veličinami (malý, vlažný, asi 5, mnoho atď.).
2.) Pokiaľ nie je známy matematický model procesu.
3.) Pokiaľ je proces výrazne nelineárny.
4.) pokiaľ sú znalosti procesu v lingvistickej forme (väčšina biologických procesov, sociálne systémy, niektoré
optimalizačné úlohy, apod.).
Fuzzy systémy vychádzajú z tzv. fuzzy logiky. Tá napĺňa nepresné formy ľudského myslenia matematickým obsahom. Na rozdiel od bežnej logiky , v ktorej môže platiť len jedna pravda (1) a nepravda (0), vo fuzzy logike existuje priestor medzi 0 a 1. hodnota 0,9 sa dá vyjadriť ako skoro istota. Takýmito spôsobmi je možné interpretovať nemetrické veličiny ako rýchlo, často, teplý, malý apod. Vo fuzzy logike sú členom určitej fuzzy množiny (na rozdiel od Boolovej logiky) priradené stupne príslušnosti (váha), vyjadrujúca nakoľko člen spĺňa podmienku príslušnosti k danej množine.
Základom riadiaceho algoritmu zostáva, ako expertných systémov 1. generácia, časť, kde sa pre generovanie akčného zásahu používa kvalitatívne formulovaná znalosť vo forme pravidiel ak podmienka, potom následok, prípadne ak podmienka 1 a podmienka 2 alebo podmienka 3, potom následok (napr. ak je mokro, potom idem pomalšie, prípadne ak je vlhko a mám ojazdené pneumatiky alebo je poľadovica, potom idem pomalšie, t.j. ak sledovaná veličina y ..., potom akčná veličina u...).
Prvým krokom spracovania vstupnej informácie musí byť teda určenie váhy vstupnej veličiny, t.j. určenie funkcie príslušnosti.
Druhým krokom je stanovenie zodpovedajúcej operácie medzi neurčitou množinou podmienkovej časti (ak...) a neurčitou množinou časti nasledovnej (potom ...0, prípadne medzi ich funkciami príslušnosti.
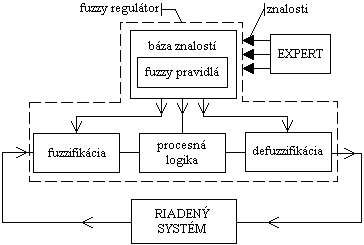
Fuzzy regulátor (obr.5.39.) alebo fuzzy expertný systém musí najprv na základe vložených inštrukcií (báze znalosti) previesť tzv. fuzzyfikáciu svojich vstupných (meraných) premenných , t.j. priradiť týmto hodnotám lingvistickú hodnotu vo forme váhy či hodnoty funkcie príslušnosti (napr. 18 °C =,,0,6 studené”), pričom záleží na vložených inštrukciách prevedených expertom aké váhy sú jednotlivým stavom prisúdené. Potom regulátor prevedie tzv. defuzzyfikáciu, t.j. prevod fuzzy hodnoty akčnej veličiny na metrickú hodnotu signálu akčnej veličiny (napr. poloha y = 0,6 zavreté).

Obr. 5.39. Bloková schéma fuzzy regulátora
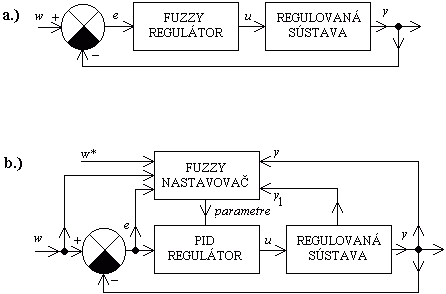
Na obr. 5.40. sú zobrazené základné množiny použitia fuzzy regulátora , a síce ako skutočného regulátora (priameho), alebo ako nastavovača štandardného regulátora (PI, PD, PID), kde je dokonca možný aj variant dodatočného vstupu operátora (w*) pre zadávanie subjektívnych ,,meraných” hodnôt obsluhou.
Tam kde postačí klasický regulátor PID, je zbytočné používať adaptívny alebo fuzzy regulátor. Typickou doménou fuzzy regulátorov sú sústavy s výraznými nelinearitami, s dopravným oneskorením, sústavy ktorých parametre sa v čase menia alebo sústavy obtiažne či vôbec neidentifikovateľné (napr. chemické procesy, ktoré v niektorej fáze teplo uvoľňujú, v niektorej naopak spotrebúvajú). Výhodné sú tiež u viacparametrovej regulácii (napr. súčasná regulácia teploty a vlhkosti v skleníku apod.).
Uvádza sa, že dobre nastavený regulátor PID je rovnocenný fuzzy regulátoru. Problém však je v tom, že málo kto vie kvalifikovane nastaviť parametre regulátora PID, zatiaľ čo dobre navrhnutý fuzzy regulátor pracuje uspokojivo aj za nevhodných podmienok. Tým sa obmedzuje nutnosť kvalifikovanej obsluhy. O to väčšie sú však nároky experta, ktorý má navrhnúť spoľahlivý a robustný fuzzy algoritmus.