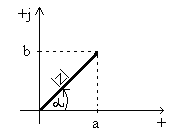
2.4 Úvod do matematického riešenia regulačných obvodov

Komplexné číslo

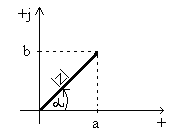
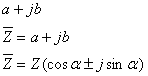
Derivácia časovej funkcie

- pri určovaní vlastností dynamických členov vyšetrujeme ich prechodové charakteristiky, čiže časové funkcie, ktoré vyjadrujeme matematicky diferenciálnymi    rovnicami

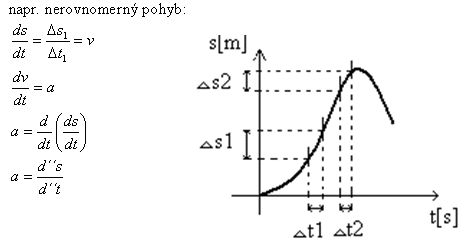
Strmosť dráhy určuje ako rýchlo sa dráha menila v časovom intervale Δt1. Aby tieto zmeny boli čo najpresnejšie zachytené, musí byť časový interval veľmi malý, a preto sa volí Δt nekonečne malé, čiže blízke nule, alebo tomu hovoríme časový diferenciál dt.

Fyzikálny význam derivácie: Fyzikálnou podstatou prvej derivácie je okamžitá rýchlosť zmeny hodnoty derivovanej veličiny. Ak je zmena nulová (veličina je

                                                konšt) derivácia je nulová. Ak derivujeme rýchlosť, dostaneme rýchlosť zmeny rýchlosti, čiže zrýchlenie pôvodnej veličiny.

Geometrický význam derivácie: je strmosť, čiže smernica krivky.

Integrácia časovej funkcie

- pri nerovnomernom pohybe je celková dráha daná súčtom všetkých jednotlivých prírastkov dráhy

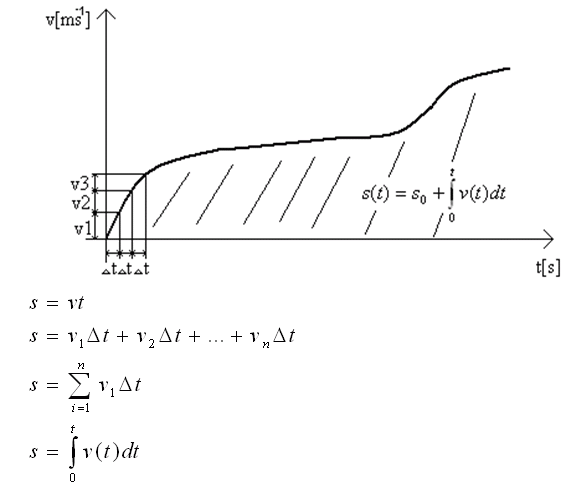
Presnosť integrácie bude tým lepšia, čím menšie bude dt → integrál je plocha medzi časovou krivkou a krivkou rýchlosti.

Geometrický význam integrácie: Je súčet plôch medzi danou funkčnou krivkou a časovou osou. Pri integrácii niekedy treba uvažovať hodnotu  

                                                       fyzikálnej veličiny pred integráciou = počiatočná podmienka integrácie

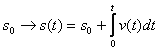
V praxi: derivácie a integrácie sa často vyskytujú pre derivovanie a integrovanie elektrických  signálov – najčastejšie cez operačný zosilňovač.