6.5 Základné logické funkcie
Typ logickej funkcie určuje výslednú hodnotu z kombinácie vstupných hodnôt. Funkcia pritom môže byť realizovaná rôzne: pomocou mechanických kontaktov, logických integrovaných obvodov, programovateľného automatu, či dokonca osobného počítača.
Prehľad dvojstupových logických funkcií
Negácia je najjednoduchšou logickou funkciou, logický člen negácie má jeden vstup a jeden výstup. Hodnota výstupu je vždy opačná k hodnote vstupu.
skratka: NOT, INV označenie: A, NOT A spojka: neplatí, že
pravdivostná tabuľka:
|
A |
Y |
|
0 |
1 |
|
1 |
0 |
Technická realizácia funkcie je na obr.6.3..
Obr. 6.3. Značky pre logickú funkciu negácie NOT
Logický súčin môže byť definovaný aj pre viacej vstupných premenných. Výsledok logického súčinu niekoľkých premenných je rovný jednej iba v prípade, keď sú všetky vstupné premenné rovné jednej.
Skratka: angl.
AND, nem. UND
označenie: A.B,
spojka: a, a zároveň, i
pravdivostná tabuľka pre dve vstupné premenné:
|
A B |
Y |
|
0 0 |
0 |
|
0 1 |
0 |
|
1 0 |
0 |
|
1 1 |
1 |
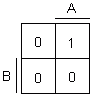
Logický súčin dvoch premenných A, B je rovný jedenej iba v prípade, že obe vstupné premenné sú zároveň rovné jednej.
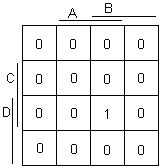
Technická realizácia logického súčinu je na obr. 6.4..
Obr. 6.4. Značky pre logický súčin AND
Poznámka:
Odporúča sa používať značky v tvare pravouholníka. Druhé značenie zodpovedá americkým zvyklostiam (Texas Instrument).
Aj logický súčet môže byť definovaný pre viacej vstupných premenných. Výsledok logického súčtu niekoľkých premenných je rovný jednej vždy, keď aspoň jedna vstupná premenná je rovná jednej.
Skratke: angl.
OR, nem. ODER
označenie: A+B,
spojka:
alebo (v zlučovacom zmysle)
pravdivostná tabuľka pre dve vstupné premenné:
|
A B |
Y |
|
0 0 |
0 |
|
0 1 |
1 |
|
1 0 |
1 |
|
1 1 |
1 |
Logický súčet dvoch premenných A, B je rovný jednej v prípade, že niektorá alebo obe vstupné premenné sú rovné jednej.
Technická realizácia logického súčtu je na obr. 6.5..
Obr. 6.5. Značky pre logický súčet OR
Negovaný logický súčin, Shefferova funkcia < >
Negovaný logický súčin môže byť definovaný aj pre viacej vstupných premenných. Výsledok negovaného logického súčinu niekoľkých premenných je rovný jednej vždy, keď aspoň jedna vstupná premenná je rovná nule.
Skratka: NAND
označenie:
pravdivostná tabuľka pre dve vstupné premenné:
|
A B |
Y |
|
0 0 |
1 |
|
0 1 |
1 |
|
1 0 |
1 |
|
1 1 |
0 |
Negovaný logický súčin dvoch premenných je rovný jednej vtedy, ak aspoň jedna vstupná premenná je rovná nule.
Technická realizácia negovaného logického súčinu je na obr. 6.6..
Obr. 6.6. Značky pre negovaný logický súčin NAND
Negovaný logický súčet, Pierceova funkcia < >
Negovaný logický súčet môže byť definovaný aj pre viac vstupných premenných. Výsledok negovaného logického súčtu niekoľkých premenných je rovný jednej iba vtedy, keď každá vstupná premenná je rovná nule.
Skratka:
NOR označenie:
spojka: ani
Pravdivostná tabuľka pre dve vstupné premenné
|
A B |
Y |
|
0 0 |
1 |
|
0 1 |
0 |
|
1 0 |
0 |
|
1 1 |
0 |
Negovaný logický súčet dvoch premenných, je rovný jednej vtedy, ak sú obe vstupné premenné rovné nule.
Technická realizácia negovaného logického súčtu je na obr. 6.7..
Obr. 6.7. značky pre negovaný logický súčet NOR
Výlučný logický súčet, exkluzívny súčet, EX–OR, XOR < >
Funkcia výlučného logického súčtu nadobúda hodnotu jedna iba v prípade, keď práve jedna zo vstupných premenných je rovná jednej. Pre dve vstupné premenné býva tiež označená ako nonekvivalencia, NEQ, súčet modulo 2, M2, mod 2 a iné.
Skratka: XOR
označenie:
spojka:
jeden alebo druhý (nie oba naraz)
pravdivostná tabuľka pre dve vstupné premenné:
|
A B |
Y |
|
0 0 |
0 |
|
0 1 |
1 |
|
1 0 |
1 |
|
1 1 |
0 |
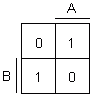
Exkluzívny logický súčet dvoch premenných je rovný jednej vtedy, ak sa líšia obe vstupné premenné.
Technická realizácia exkluzívneho logického súčtu je na obr. 6.8..
Obr. 6.8. Značky pre exkluzívny logický súčet XOR
Prehľad dvojvstupových logických funkcií < >
Na záver uvádzame prehľad všetkých šestnástich dvojvstupových logických funkcií (vstupy A, B, výstup Y) aj s ich názvami.
|
A |
B |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
Y8 |
Y9 |
Y10 |
Y11 |
Y12 |
Y13 |
Y14 |
Y15 |
Y16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Tab. 6.2.a Pravdivostná tabuľka v všetkých logických funkcií
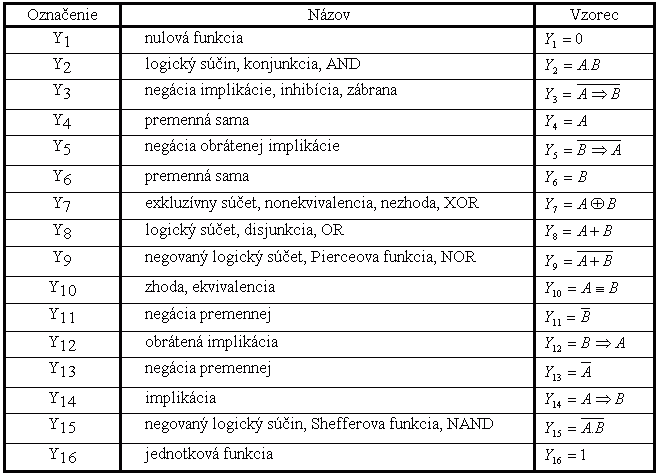
Tab. 6.2.b Prehľad všetkých logických funkcií
