7.10 Diferenčné rovnice

Popisuje aké budú hodnoty výstupného signálu y(k) v okamihoch k= 1,2,3,....

    Koeficienty a_i , b_i vyjadrujú vlastnosti sústavy (T₁ , K_S) a závisia aj od periódy vzorkovania (T). Číselné hodnoty koeficientov a_i , b_i platia iba pre určitú periódu vzorkovania, b_i iba pre určitý tvarovač (v našom prípade nultého rádu).

Novú hodnotu y(k) vypočítame z hodnoty vstupu u(k–1) a výstupu y(k–1) v minulom vzorkovaní. Pre danú sústavu S môžeme vytvoriť nekonečne veľa diferenčných rovníc líšiacich sa periódou vzorkovania T. Diferenčné rovnice vyšších rádov môžeme vyjadriť obdobne:

Diferenčná rovnica sústavy n–tého rádu:

Riešenie diferenčnej rovnice:

Poznáme dve metódy:

1. Numerické riešenie: postupne  sa  vypočítavajú  hodnoty  výstupného  signálu y(k),tak aby sa objavovali na výstupe sústavy v okamihoch k= 1,2,3,.... Musíme mať    všetky predchádzajúce vzorky. Táto metóda je vhodná pre počítače alebo mikropočítače, ktoré neriešia rovnicu sústavy, ale počítajú rovnicu regulátora. 

2. Riešenie transformáciou Z: Z transformácia  je  zložitý  matematický aparát, ktorý je obdobou Laplaceovej transformácie. Výsledkom je všeobecný vzťah, do ktorého sa dosadí poradové číslo vzorky a hodnoty y(k) sa priamo vypočíta.

Príklad 2: Regulovaná sústava je popísaná diferenčnou rovnicou:. Vyšetrite jej odozvu  na impulz u(k) podľa priebehu:

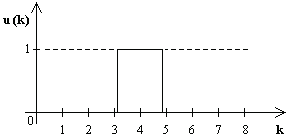
                                                                                     Obr. 7.12. Impulz akčnej veličiny

                        Riešenie:   

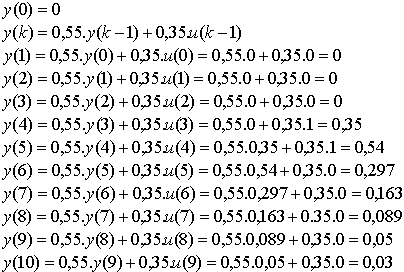
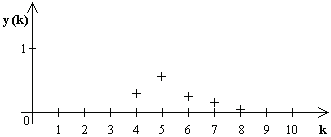
Obr.7.13. Odozva regulovanej sústavy na impulz akčnej veličiny z obr. 7.12.